Confirmatory Bayesian Online Change Point Detection in the Covariance Structure of Gaussian Processes

Jiyeon Han*, Kyowoon Lee*, Anh Tong, Jaesik Choi

IJCAI 2019

(*: equal contribution)

[Paper] [Poster]

Abstract

In the analysis of sequential data, the detection of abrupt changes is important in predicting future events. In this paper, we propose statistical hypothesis tests for detecting covariance structure changes in locally smooth time series modeled by Gaussian Processes (GPs). We provide theoretically justified thresholds for the tests, and use them to improve Bayesian Online Change Point Detection (BOCPD) by confirming statistically significant changes and non-changes. Our Confirmatory BOCPD (CBOCPD) algorithm finds multiple structural breaks in GPs even when hyperparameters are not tuned precisely. We also provide conditions under which CBOCPD provides the lower prediction error compared to BOCPD. Experimental results on synthetic and real-world datasets show that our proposed algorithm outperforms existing methods for the prediction of nonstationarity in terms of both regression error and log likelihood.

Contribution

• We propose new statistical likelihood ratio tests that detect changes in the covariance structure of GPs and provide thresholds and conditions under which we can guarantee the bounded test error.
• We build a theoretically justified online detection algorithm, Confirmatory BOCPD, which detects CPs with a reasonable time delay. We also present sufficient conditions under which CBOCPD provides the lower prediction error compared to BOCPD.
• Our algorithm adjusts the parameter of BOCPD to avoid false alarms and missed detections when the results of hypothesis tests are sound. When the results are not sound, our algorithm takes advantages of Bayesian inference from BOCPD.

Change Point Detection in the Covariance Structure of GPs

The following figure shows how CPD of a covariance structure could affect the quality of a GP regression. The left plot in the figure shows samples from a GP with an intended CP in the middle. The middle plot shows samples from a GP model after the hyperparameters have been learnt using the whole datasets. The right plot shows samples from a GP model whose covariance structure breaks and the hyperparameters have been learnt separately. The following figure suggests that fitting nonstationary data to a time-invariant GP results in an imprecise model. GP regression with a structural break in the covariance structure is more expressive and better suited to the analysis of nonstationary data.

To construct a test for detecting changes in the covariance structure, we define the null hypothesis as \(\mathbb{H}_0: \mathrm{Cov}(X_i,X_j) = K(i,j)\) and the alternative hypothesis as \(\mathbb{H}_{1}=\bigcup_{t\in \mathcal{C}_{n}}\mathbb{H}_{1,t}\) with

where \(K\), \(K′\) and \(K”\) are the kernel functions.

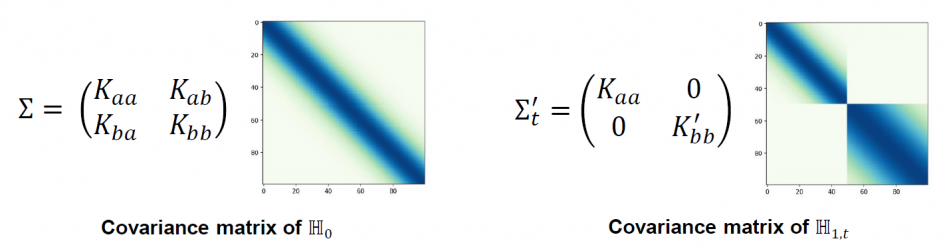
Let \(\Sigma\) and \(\Sigma_t'\) denote the covariance matrices for \(\mathbb{H}_0\) and \(\mathbb{H}_{1,t}\), respectively. The likelihood ratio \(2\mathfrak{L}\) is written as

We now define a likelihood ratio test as \(\mathfrak{T}_{GLRT} = \mathbb{I}\left( 2\mathfrak{L} \ge \mathfrak{R}_{\delta} \right)\). With a proper threshold \(\mathfrak{R}_{\delta}\), the detection error probability is bounded below by a predefined error bound \(\delta\).

Confirmatory Bayesian Online Change Point Detection

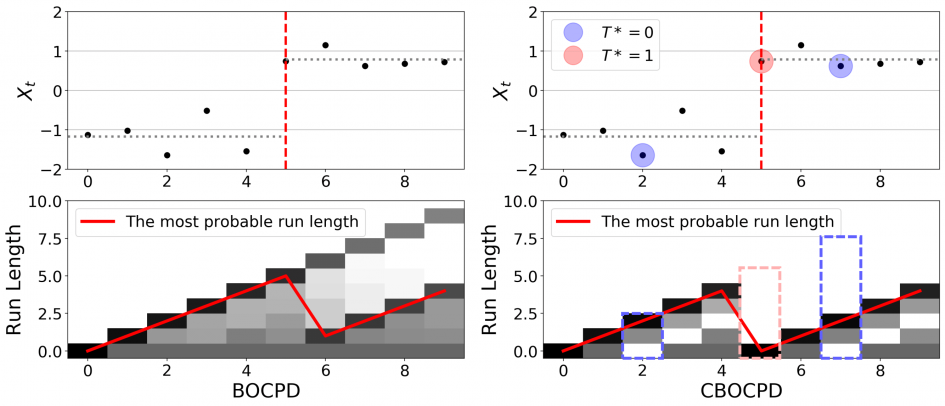
We present a theoretically justified online change detection algorithm, CBOCPD. The main idea of CBOCPD is to overcome the limitations of the assumption that the run length is independent of the data. We claim that the run length distribution given data can be more precisely calculated by using the likelihood ratio test. The likelihood ratio tests are applied to the window. If the likelihood ratio test passes at t, we decide that t is a change point and increase the probability that run length rt=0, which enhances the probability of change in the BOCPD framework. In contrast, if test does not pass, we strongly believe there is no change and reduce the probability of change in the BOCPD framework. This is why we name this algorithm Confirmatory BOCPD.

C-BOCPD is less sensitive to the hyperparameter

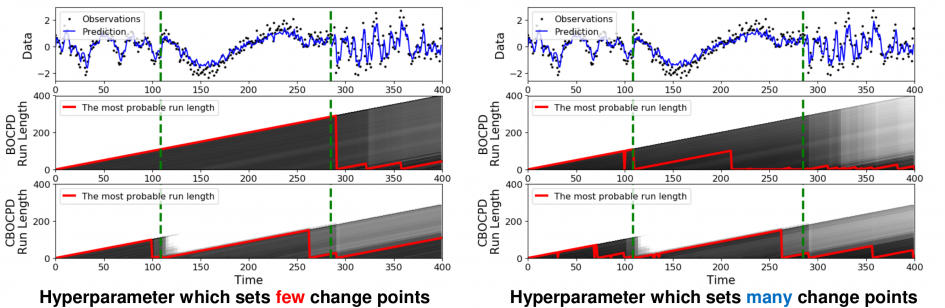
The above figures show synthetic data (top) with two changes in hyperparameters of GP and the derived run-length distribution computed from BOCPD (middle) and CBOCPD (bottom). Dashed green line indicates the true CPs. The above figures show that CBOCPD identifies the length scale change in the data with the help of statistical tests, whereas BOCPD captures the change too less or too many times.

Dataset

We use two synthetic datasets generated by GPs with changes in the length scale and the variance of a Radial Basis Function kernel, respectively. Observations are obtained by adding the white Gaussian noise with the variance \(\sigma^2_{no}=0.1\). For both datasets, two CPs are drawn uniformly from time intervals \((75, 125)\) and \((275, 325)\) with end time \(T=400\). We also use Gazebo Robot Simulation Data under the changing environment of the floor. For the real world time series datasets, we use Nile Data (200 training points, 463 test points), Well Log Data (500 training points, 3050 test points), and Snow Data (500 training points, 13380 test pionts).

Reference

@inproceedings{han2019confirmatory,
title={Confirmatory Bayesian Online Change Point Detection in the Covariance Structure of Gaussian Processes},
author={Han, Jiyeon and Lee, Kyowoon and Tong, Anh and Choi, Jaesik},
booktitle={The 28th International Joint Conference on Artificial Intelligence},
pages={2449–2455},
year={2019},
organization={International Joint Conference on Artificial Intelligence (IJCAI)}
}