Deep Reinforcement Learning in Continuous Action
Spaces: a Case Study in the Game of Simulated Curling

Kyowoon Lee*, Sol-A Kim*, Jaesik Choi, Seong-Whan Lee

ICML 2018

(*: equal contribution)

[Paper] [Code] [Poster]

Abstract

Many real-world applications of reinforcement learning require an agent to select optimal actions from continuous spaces. Recently, deep neural networks have successfully been applied to games with discrete actions spaces. However, deep neural networks for discrete actions are not suitable for devising strategies for games where a very small change in an action can dramatically affect the outcome. In this paper, we present a new self-play reinforcement learning framework which equips a continuous search algorithm which enables to search in continuous action spaces with a kernel regression method. Without any hand-crafted features, our network is trained by supervised learning followed by self-play reinforcement learning with a high-fidelity simulator for the Olympic sport of curling. The program trained under our framework outperforms existing programs equipped with several hand-crafted features and won an international digital curling competition.

Contribution

• We present a new framework which incorporates a deep neural network for learning game strategy with a kernel-based Monte Carlo tree search from a continuous space.
• Without the use of any hand-crafted feature, our policy-value network is successfully trained using supervised learning followed by reinforcement learning with a high-fidelity simulator for the Olympic sport of curling.
• The program trained under our framework outperforms existing programs equipped with several hand-crafted features and won an international digital curling competition.

Learning in the Discretized Action Space with Kernel Method

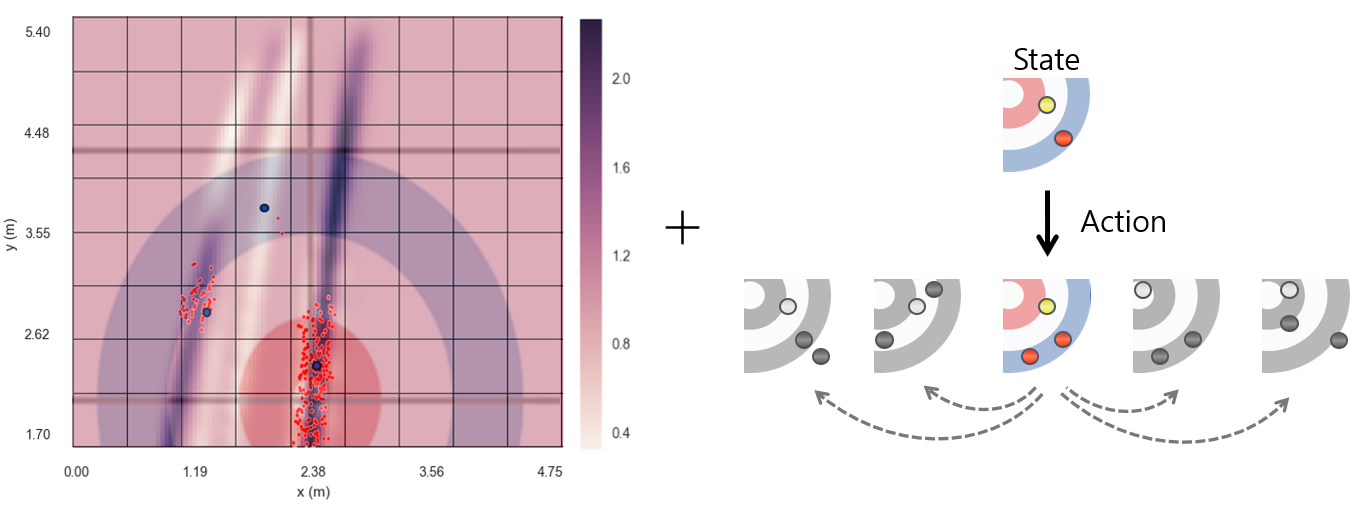
• Conducts local search with continuous action samples generated from a deep convolutional neural network (CNN).
• Generalizes the information between similar actions through kernel methods.

Kernel Regression Deep Learning UCT

Our policy-value network takes the following inputs; the stones’ location, the order to tee, the number of shots, and flags to indicate whether each grid cell inside of the house is occupied by any stone. After the first convolutional block, the nine residual blocks follow, which are shared during training procedure. We train the policy and the value functions in a unified network. The output of the policy head is the probability distribution of each action. The output of the value head is the probability distribution of the final scores \([-8, 8]\).

In the proposed KR-DL-UCT algorithm, the expected value and the number of visits is estimated by kernel density estimation and kernel regression respectively.

In the selection step, we used Upper Confidence Bound (UCB) as selection function to handle trade-off between exploitation and exploration. This selection function encourages exploration in actions with high variance and moderate expected reward.

In the expansion step, to explore actions in continuous action space outside of the initialized actions by policy network, we find a new continuous action sample which minimizes the kernel density estimate within whose kernel weight is at least some threshold. This procedure can be approximated by sampling actions around the selected action and choosing the one with the minimal kernel density.

Dataset

In this paper, we use simulated curling software which assumes a stationary curling sheet. Thus, ice conditions are assumed to remain unchanged, the sweeping is not considered, and asymmetric Gaussian noise is added to the every shot. The simulator is implemented using the Box2D physics library, which deals with the trajectory of the stones and their collisions

• Supervised Learning: 0.4 million of the play data from the champion program (AyumuGAT’16) of Game AI Tournaments (GAT) digital curling championship in 2016.
• Self-play Reinforcement Learning: 5 million of the play data from self-play matches of KR-DL-UCT, executing 400 simulations per move.

Experiments

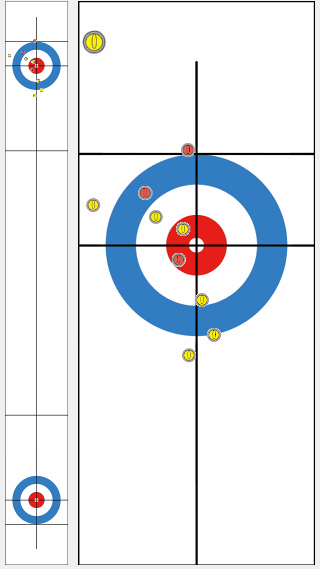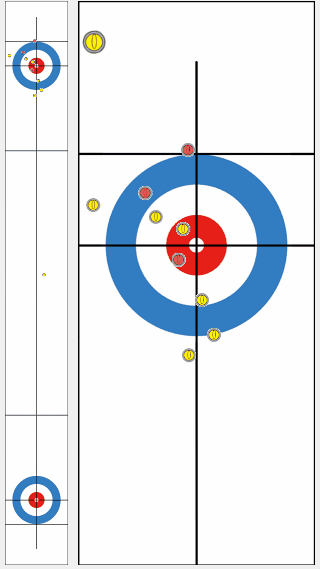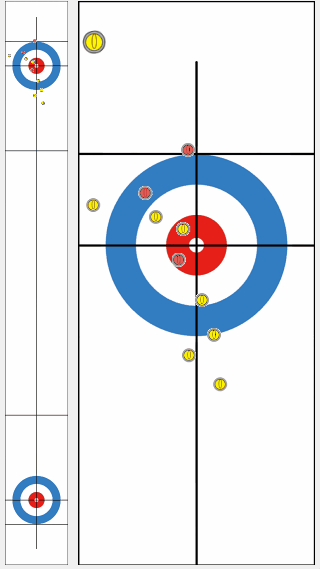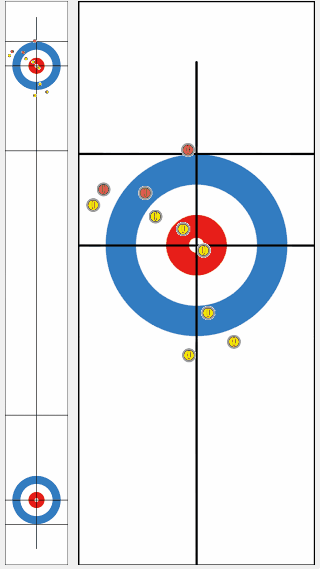
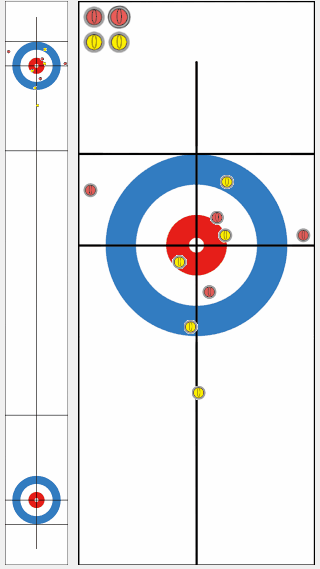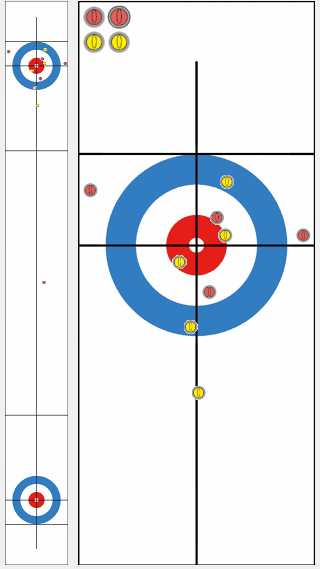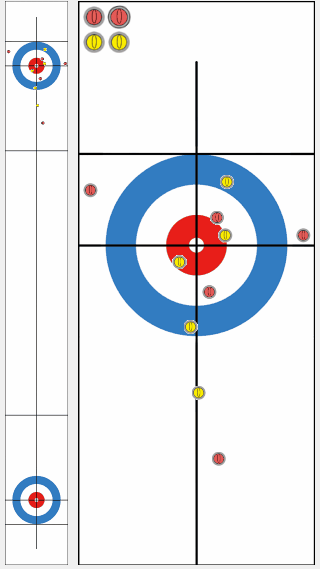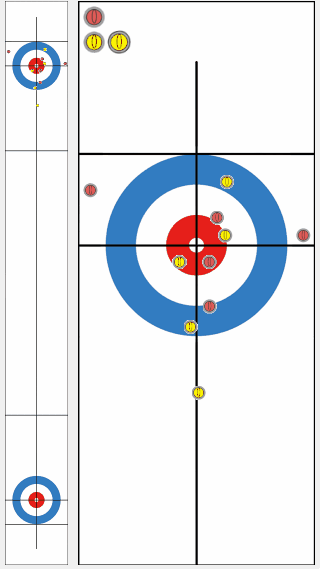
We compared the performance of a program trained by our proposed algorithm KR-DL-UCT with a baseline program DL-UCT trained without kernel methods. We initialized both models with the supervised learning and then trained further from shots of self-play games with two different algorithms. With the supervised training only, the KR-DL-UCT wins about 53% against DL-UCT. Further, KR-DL-UCT expedites the training procedure by improving the overall performance compared to DL-UCT under the self-play RL framework. After gathering 5 million shots from self-play, KR-DL-UCT wins 66% which is significantly higher than the winning percentage of DL-UCT.

• KR-DL: KR-DL-UCT with supervised learning
• KR-DRL: KR-DL with self-play RL
• KR-DRL-MES: KR-DRL with winning percentage table (multi-end strategy)

Our program KR-DRL-MES won in the international digital curling competition, GAT-2018.

Reference

@inproceedings{lee2018deep,
  title={Deep reinforcement learning in continuous action spaces: a case study in the game of simulated curling},
  author={Lee, Kyowoon and Kim, Sol-A and Choi, Jaesik and Lee, Seong-Whan},
  booktitle={International conference on machine learning},
  pages={2937--2946},
  year={2018},
  organization={PMLR}
}